$e^x x$<<1の時の近似

まず$\mathrm{e}^x$をマクローリン展開してみる

$$ f(x) = \mathrm{e}^x $$ とおいて

$$ f’(x) = \mathrm{e}^x \\ f^2(x) = \mathrm{e}^x $$ マクローリン展開は $$ f(x) = \frac{f(0)}{0!}+\frac{f^1(0)}{1!}x+\frac{f^2(0)}{2!}x^2+\cdots $$

なので $$ e^x = 1+x+\frac{1}{2}x^2+\frac{1}{6}x^3+\cdots $$

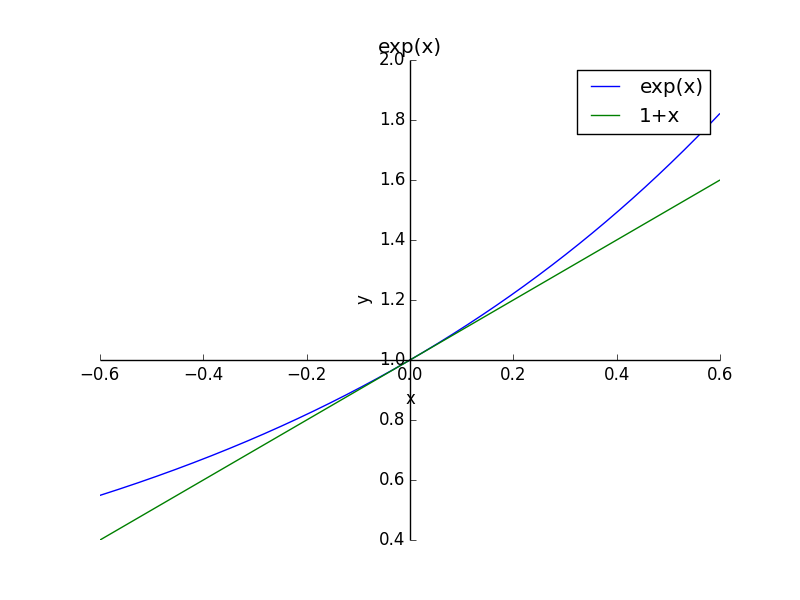
$x\ll1$の時 $$ e^x = 1+x $$ と近似できる。このことは以下のグラフを見ると明らかである。